Üçgende kosinüs teoremi:

ABC Üçgeninde ; kenarlar arasında ,

a² = b² + c² - 2 . b . c .Cos A

b² = a² + c² - 2 . a . c .Cos B

c² = a² + b² - 2 . a . b .Cos C

eşitlikleri vardır.

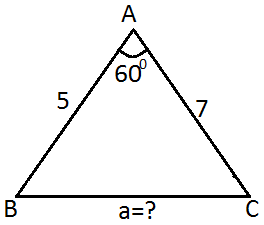
1)

Şekildeki üçgende verilenlere göre a = ? kaçtır?

Çözüm:

Kosinüs teoremi uygulanırsa ,

a² = b² + c² - 2 . b . c .Cos A

a² = 7² + 5² - 2 . 7 . 5 .Cos 60

a² = 49 + 25 - 70 . (1/2)

a² = 74 - 35

a² = 39

a = √39

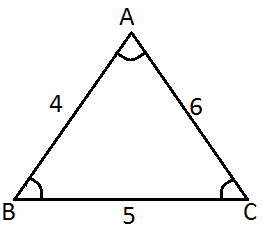
2)

Şekildeki üçgende verilenlere göre Cos A = ? nedir?

Çözüm:

Kosinüs teoremi uygulanırsa ,

a² = b² + c² - 2 . b . c .Cos A

5² = 6² + 4² - 2 . 6 . 4 .Cos A

25= 36 + 16 - 48 .Cos A

25= 52 - 48 .Cos A

48 .Cos A = 52 - 25

48 .Cos A = 27

Cos A = 27 / 48

Cos A = 9 / 16

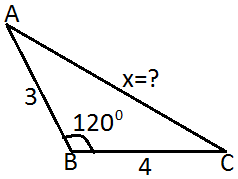
3)

Şekildeki üçgende verilenlere göre x = ? kaçtır?

Çözüm:

Kosinüs teoremi uygulanırsa ,

x² = 3² + 4² - 2 . 3 . 4 .Cos 120

x² = 9 + 16 - 24 . (-1/2)

x² = 25 + 12

x² = 37

x = √37

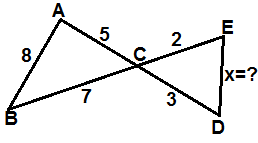
4 )

Şekildeki üçgende verilenlere göre x = ? kaçtır?

Çözüm:

Her iki üçgende C iç açısı ortak olup ters açıdan eşittir.

ABC üçgeninde Kosinüs teoremi uygulanırsa ,

8² = 5² + 7² - 2 . 5 . 7 .Cos C

64 = 25 + 49 - 70. Cos C

70. Cos C = 74 - 64

Cos C = 10 / 70

Cos C = 1 / 7

CDE üçgeninde kosinüs teoremi uygulayıp ,

Cos C yerine 1/7 yazılır.

x ² = 2² + 3² - 2 . 2 . 3 . 1 /7

x² = 4 + 9 - 12 / 7

x² = 13 - 12 / 7

x² = 91 - 12 / 7

x² = 79 / 7

x = √( 79 / 7 )