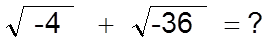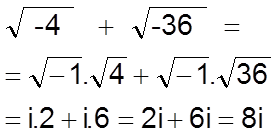Karmaşık sayıların eşitliği, karmaşık sayılarda toplama , çıkarma , çarpma , bölme
işlemleri, karmaşık sayının tersi , i nin kuvvetleri soru çözümleri bulunmaktadır.
KARMAŞIK SAYILAR
1) i2 = -1 olduğuna göre , ( 1 + i ) 15 = ?
|
Çözüm: ( 1 + i ) 2 = ( 1 + i ) . ( 1 + i ) = 1 + i + i + i2 = = 1 + 2 i - 1 = 2 i ( 1 + i ) 15 = [ ( 1 + i ) 2 ] 7 . ( 1 + i ) = = [ 2 i ] 7 . ( 1 + i ) = 2 7 . i 7 .( 1 + i ) = = 2 7 . ( - i ) . ( 1 + i ) = 2 7 . ( - i + i2 ) = = 2 7 . ( -1 - i ) |
|
2) z = 5 + 3 i , ise z . z̄ = ?
|
Çözüm: z = a + b i , ise z . z̄ = a 2 + b 2 dir. z . z̄ = 5 2 + 3 2 = 25 + 9 = z . z̄ = 34 |
|
3) z 1 = 8 - 5 i ve z 2 = 2 + 3 i , ise z 1 + z 2 =?
|
Çözüm: Karmaşık sayılarda toplama işlemine göre, reel kısımlar reel kısımlarla , sanal kısımlarda sanal kısımlarla ( i ' li olan) toplanır. z 1 + z 2 = 8 - 5 i + 2 + 3 i z 1 + z 2 = 10 - 2 i |
|
4) z 1 = -4 + 9 i ve z 2 = - 11 + 4 i , ise z 1 - z 2 =?
|
Çözüm: Karmaşık sayılarda çıkarma işlemine göre, z 1 - z 2 = ( -4 + 9 i ) - ( - 11 + 4 i ) z 1 - z 2 = -4 + 9 i + 11 - 4 i z 1 - z 2 = 7 + 5 i |
|
5) z = 3 + 5 i , karmaşık sayısının çarpmaya göre tersi nedir? z - 1 =?
|
Çözüm: Karmaşık sayının tersi formüle göre , z = a + b i , ise z - 1 = [ a / a 2 + b 2 ] - [ b / a 2 + b 2 ] .i Yukarıdaki formüle göre , z - 1 = [ 3 / 3 2 + 5 2 ] - [ 5 / 3 2 + 5 2 ] .i z - 1 = [ 3 / 34 ] - [ 5 / 34 ] .i z - 1 = 1 / 34 . [ 3 - 5 i ] |
|
- Karmaşık Sayılar
- Read Time: 1 min
- Gösterim: 12089