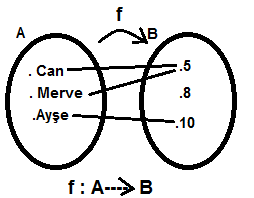FONKSİYONLAR
Yukarıdaki şekilde fonksiyonun soruda verilen kuralına göre ,
tanım kümesindeki elemanlara karşılık gelen görüntü değerlerine yapılan eşlemeler görülmektedir.
Görüntü kümesi olan f (A) kümesindeki sıralı ikililer , dik koordinat düzleminde yerleri belirlenerek doğrusal fonksiyonun grafiği çizilebilir. Grafik çizimi için doğru grafiği çizme sayfasını inceleyebilirsiniz.
Soru 1
f ( x ) = x + 7 ise f ( 4 ) = ?
Çözüm :
Fonksiyonda x in yerine 4 yazılır.
f ( 4 ) = 4 + 7
f ( 4 ) = 11
Soru 2
f ( x ) = 3 x + 5 ise f ( 8 ) = ?
Çözüm :
Fonksiyonda x in yerine 8 yazılır.
f ( 8 ) = 3 . 8 + 5
f ( 8 ) = 24 + 5
f ( 8 ) = 29
Soru 3
f ( x ) = 2x - 5 ise f ( -7 ) = ?
Çözüm :
Fonksiyonda x in yerine -7 yazılır.
f ( -7 ) = 2 . (-7) - 5
f ( -7 ) = -14 - 5
f ( -7 ) = -19
Soru 4
f ( x ) = x + 5 ise f ( x+8 ) = ?
Çözüm :
Fonksiyonda x in yerine x+8 yazılır.
f ( x+8 ) = x + 8 + 5
f ( x + 8) = x + 13
Soru 5
f ( x ) = 4x - 7 ise f ( 5x ) = ?
Çözüm :
Fonksiyonda x in yerine 5x yazılır.
f ( 5x ) = 4.(5x) - 7
f ( 5x ) = 20x - 7
Soru 6
f ( x ) = 3x - 24 ise f ( 5x + 7 ) = ?
Çözüm :
Fonksiyonda x in yerine 5x+7 yazılır.
3 parantezin içindekilerle çarpılır.
f ( 5x+7 ) = 3.(5x+7) - 24
f ( 5x+7 ) = 15x + 21 - 24
f ( 5x+7 ) = 15x - 3
Soru 7
f ( x ) = -7x - 8 ise f ( 2x+4 ) = ?
Çözüm :
Fonksiyonda x in yerine 2x+4 yazılır.
f ( 2x+4 ) = -7.(2x+4) - 8
f ( 2x+4 ) = -14x - 28 - 8
f ( 2x+4 ) = -14x - 36
Soru 8
f ( x+2 ) = x -9 ise f ( 7 ) = ?
Çözüm :
x+2 , 7 ye eşitlenip x çekilir.
Fonksiyonda x in yerine 5 yazılır.
x+2=7
x=7-2
x=5
f ( 5+2 ) = 5 -9
f ( 7 ) = -4
Soru 9
f ( x-3) = 5x -7 ise f ( 8 ) = ?
Çözüm :
x-3 , 8 e eşitlenip x çekilir.
Fonksiyonda x in yerine 11 yazılır.
x-3=8
x=8+3
x=11
f ( 11-3 ) = 5.11 -7
f ( 8 ) = 55-7
f ( 8 ) = 48
Soru 10
f ( 3x-1) = 4x +9 ise f ( 5 ) = ?
Çözüm :
3x-1 , 5 e eşitlenip x çekilir.
Fonksiyonda x in yerine 2 yazılır.
3x-1=5
3x=5+1
3x=6
x=6/3
x=2
f ( 3.2-1 ) =4.2 +9
f ( 6-1 ) = 8+9
f ( 5 ) = 17
Soru 11
f ( 2x-7) = 3x - 4 ise f ( -19 ) = ?
Çözüm :
2x-7 , -19 a eşitlenip x yalnız bırakılır.
Fonksiyonda x in yerine -6 yazılır.
2x-7=-19
2x=-19+7
2x=-12
x=-12/2
x=-6
f ( 2.(-6)-7 ) =3.(-6) - 4
f ( -12- 7) = -18 - 4
f ( -19 ) = -22
Soru 12
f ( x) = x+5 ise f - 1 ( 13) = ?
Çözüm :
Ters fonksiyon söz konusu ise
x+5 , 13 e eşitlenip x çekilir.
Fonksiyonda x in yerine 8 yazılır.
x+5= 13
x=13-5
x=8
f ( x ) =x+5 ise
x= f - 1 ( x+5 )
8= f - 1 ( 8+5 )
8= f - 1 ( 13 )
Soru 13
f ( x) = 3x-2 ise f - 1 ( -14) = ?
Çözüm :
3x-2 , -14 e eşitlenip x çekilir.
Fonksiyonda x in yerine -4 yazılır.
Aslında -4 cevaptır.
3x-2= -14
3x=-14+2
3x=-12
x=-12/3
x=-4
f ( x ) =3x - 2 ise
x= f - 1 ( 3x-2 )
-4= f - 1 ( 3.(-4)-2 )
-4= f - 1 ( -12-2 )
-4= f - 1 ( -14 ) olduğu görülür.
Soru 14
f (2x-1) = 3x-7 ise f - 1 (5 ) = ?
Çözüm :
3x-7 , 5 e eşitlenip x çekilir.
Fonksiyonda x in yerine 4 yazılır.
3x-7= 5
3x=5+7
3x=12
x=12/3
x=4
f (2 x -1) =3x -7 ise
2x-1= f - 1 ( 3x-7 )
2.4 - 1= f - 1 ( 3.4 - 7 )
8 - 1= f - 1 ( 12 - 7 )
7= f - 1 ( 5 ) olduğu görülür.yada
f - 1 ( 5 ) = 7 olur.
FONKSİYONLAR
A ve B boştan farklı iki küme olmak üzere ,
A X B kartezyen kümesinin alt kümelerine bağıntı denir.
Bu bağıntılar aşağıdaki iki koşulu sağlaması halinde A dan B ye fonksiyondur denir.
Fonksiyon olma şartları ;
A tanım kümesi ve B değer kümesi olsun .
1) Tanım kümesindeki her eleman mutlaka eşlenmeli , eşlenmeyen eleman kalmamalıdır.
2) Tanım kümesindeki her elemanın sadece bir görüntüsü olmalı ve bir kez eşlenmelidir .
Buna pratik örnek verecek olursak ,
Her çocuğun bir yaşı vardır .
Tanım kümesindeki elemanlar çocuklar olsa , Değer kümesi ise yaşları olmaktadır.
Dikkat edilecek olursa farklı çocukların aynı yaşta olabilmektedir.