Üçgende açılar ve özellikleri konusu 7. Sınıfta , 9. Sınıfta , lgs yks tyt ayt gibi sınavlarda sorulmaktadır.
Üçgende Açı sorularını çözebilmek için üçgenin iç açıları , dış açıları, ikizkenar üçgende taban açıları, eşkenar üçgende eşit açılar ve bunların köşelerinden çizilen açıortay , kenarortay, yükseklik gibi üçgenin yardımcı elemanlarının oluşturabileceği açıların özelliklerinin de bilinmesi gerekiyor.
Üçgende açılar konusunu iyi anlamak ve soruları çözebilmek için , üçgende açıortay , kenarortay ve üçgenin açıları ve kenarları arasındaki bağıntıların anlatıldığı diğer sayfalarıda incelemeniz faydalı olacaktır.
Soru 1
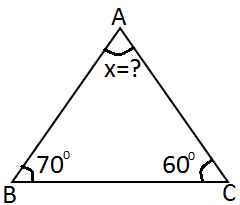
Şekildeki üçgende verilenlere göre
m ( B ) =x açısı kaç derecedir?
Çözüm:
Üçgende iç açılar toplamı 180 derece olduğundan;
x + 70 + 60 = 180
x + 130 = 180
x = 180 - 130
x = 50 derece olur.
Soru 2
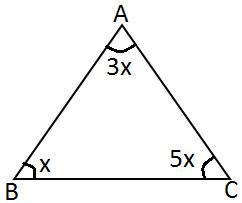
Şekildeki üçgende verilenlere göre
m ( B ) =x açısı kaç derecedir?
Çözüm:
Üçgende iç açılar toplamı 180 derece olduğundan;
x + 3x + 5x = 180
9x = 180
x = 180 / 9
x = 20 derecedir.
Soru 3
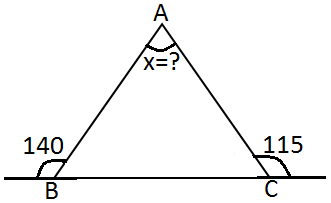
Şekildeki üçgende verilenlere göre
m ( A ) =x açısı kaç derecedir?
Çözüm:
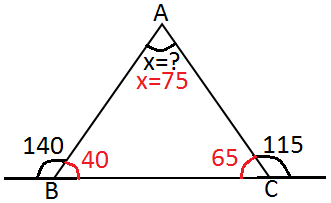
m ( B ) = 180 - 140 = 40 ,
m ( C ) = 180 - 115 = 65
Üçgende iç açılar toplamı 180 derece olduğundan;
x + 40 + 65 = 180
x + 105 = 180
x = 180 - 105
x = 75 derece olur.
Soru 4

Şekildeki üçgende verilenlere göre
m ( C ) = x açısı kaç derecedir?
Çözüm:
Üçgende iki iç açının toplamı
diğer köşedeki dış açıya eşit olur.
x = 80 + 50
x = 130
Soru 5
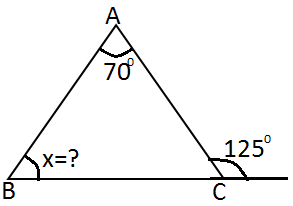
Şekildeki üçgende verilenlere göre
m ( B ) =x açısı kaç derecedir?
Çözüm:
Üçgende iki iç açının toplamı
diğer köşedeki dış açıya eşit olur.
x + 70 = 125
x = 125 - 70
x = 55
Soru 6
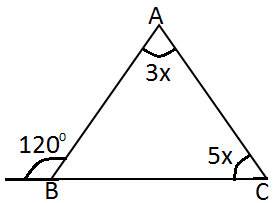
Şekildeki üçgende verilenlere göre
m ( A ) açısı kaç derecedir?
Çözüm:
Üçgende iki iç açının toplamı
diğer köşedeki dış açıya eşit olur.
3x + 5x = 120
8 x = 120
x = 120 / 8
x = 15 olup , m ( A ) = 3x = 3 . 15 = 45 olur.
Soru 7
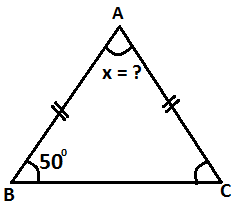
Şekildeki üçgende | AB | = |AC | , m(B)=50 ise ,
m ( ABC ) = x kaç derecedir?
Çözüm :
İkizkenar üçgende taban açıları eşit olur. m(ACB )=50 olur.
x = 180 - ( 50 + 50 ) =
x = 180 - 100
x = 80
Soru 8
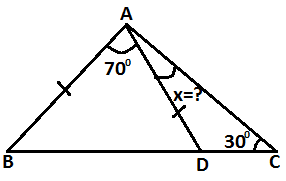
Şekildeki üçgende verilenlere göre
x kaç derecedir?
Çözüm :
İkizkenar üçgende tepe açısı verilmiş,
taban açılarını bulmalıyız.
m ( D ) = (180 - 70 ) / 2 = 55 olur.
İki iç açının toplamı , diğer dış açıyı verir.
x + 30 = 55 ise
x = 25
Soru 9
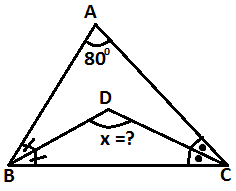
Çözüm :
Taban açılarına a,a ve b,b diyelim .
2a + 2b + 80 = 180
2 . ( a + b ) = 180 - 80
a + b = 100 / 2
a + b = 50 olur .
Küçük üçgende iç açılar toplamı 180 ,
a + b + x = 180
x = 180 - 50
x = 130 .
2. yol :
İki iç açıortayın kesim noktasındaki açı ,
90 + ( m(A ) ) / 2 dir.
x = 90 + 80 / 2 = 130 olur.
PDF indirmek için tıklayın
Üçgende Açılar Çözümlü sorular 1 pdf indirmek için tıklayın.
Devamı ..Üçgende Açılar Çözümlü Sorular 2
| Devamı .. | |||
| Üçgende Açılar Çözümlü Sorular 1 | Üçgende Açılar Çözümlü Sorular 2 | Üçgende Açılar Çözümlü Sorular 3 | Üçgenler Çözümlü Sorular Tümü |
