iki nokta arasındaki uzaklık, iki doğru arası uzaklık bulma.
1) A ( x - 3 , y + 5 ) noktası dik koordinat düzleminde 2. bölgede ise, x ve y hangi aralıkta olur ? |
Çözüm : Analitik düzlemde ikinci bölgede , ( - , + ) olup , x < 0 ve y > 0 dır. Buna göre , Birinci bileşen , x - 3 < 0 ise x < 3 İkinci bileşen , y + 5 > 0 ise y > -5 olur.
|
|||||||||||||||||
2) A ( 2 , 5 ) noktasından geçen ve , y = 3 x + 11 doğrusuna paralel olan doğrunun denklemi nedir?
|
Çözüm : Denklemi istenen doğru soruda verilen doğruya paralel olacaksa , eğimleri aynı olmalıdır. Buna göre , y = 3 x + 11 doğrusunun eğimi 3 olup , A ( 2 , 5 ) noktasından geçen ve eğimi 3 olan doğru , Eğimi ve bir noktası bilinen doğru denklemi ile bulunur. y - y1 = m . ( x - x1 ) y - 5 = 3 . ( x - 2 ) y - 5 = 3x - 6 y = 3x - 6 + 5 y = 3x -1 olur. yada 0 = 3x - y - 1 şeklinde de olabilir. |
|||||||||||||||||
3) A ( 7 , 3 ) noktasından geçen ve , y = 5 x - 2 doğrusuna dik olan doğrunun denklemi nedir?
|
Çözüm : Denklemi istenen doğru, soruda verilen doğruya dik olacaksa , eğimleri çarpımı -1 olmalıdır. Buna göre , y = 5 x - 2 doğrusunun eğimi 5 olup , A ( 7 , 3 ) noktasından geçen ve eğimi - 1 / 5 olan doğru , Eğimi ve bir noktası bilinen doğru denklemi ile bulunur. y - y1 = m . ( x - x1 )
5 y - 15 = - x + 7 5 y - 15 + x + 6 = 0 x + 5y - 9 = 0 |
|||||||||||||||||
4) A ( - 4 , 1 ) noktasından geçen ve , 3x - 5y + 8 = 0 doğrusuna dik olan doğrunun denklemi nedir?
|
Çözüm : Denklemi istenen doğru, soruda verilen doğruya dik olacaksa , eğimleri çarpımı -1 olmalıdır. Buna göre , 3x - 5y + 8 = 0 doğrusunun eğimi - ( 3 / - 5 ) = 3 / 5 olup , çarpımı -1 olan sayı - 5 / 3 dir. A ( - 4 , 1 ) noktasından geçen ve eğimi - 5 / 3 olan doğru , Eğimi ve bir noktası bilinen doğru denklemi ile bulunur. y - y1 = m . ( x - x1 )
3 y - 3 = - 5 x - 20 3 y - 3 + 5 x + 20 = 0 5 x + 3 y + 17 = 0 şeklinde olur. |
|||||||||||||||||
5) A( -5 , -2 ) ve B ( 3 , 7 ) noktalarından geçen , AB doğrusunun eğimi nedir?
|
Çözüm : İki noktası bilinen yada verilen doğrunun eğimini bulma sorusu oluyor. Formüle göre ,
|
|||||||||||||||||
6) A ( 2 , 5 ) ve B ( 3 , 7 ) noktaları için , [AB] doğru parçasını ,|A C | / | C B | = 4 oranında içten bölen C ( x , y ) noktasının koordinatları nedir?
|
Çözüm : İçten bölen nokta formülü yardımıyla ,
C ( 14/5 , 33 / 5 ) olur. |
|||||||||||||||||
7) A ( 4 , 2 ) ve B ( 5 , 9 ) noktaları için , [AB] doğru parçasını ,|A C | / | C B | = 3 oranında dıştan bölen C ( x , y ) noktasının koordinatları nedir?
|
Çözüm : Dıştan bölen nokta formülü yardımıyla ,
C ( 11 / 2 , 25 / 2 ) olur. |
|||||||||||||||||
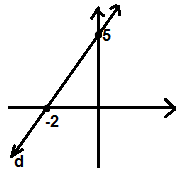
8)
Şekilde verilen d doğrusunun eğimi kaçtır?
|
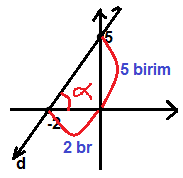
Çözüm :
Grafiği verilen doğrunun eğimi, Doğrunun x ekseni ile pozitif yönde (saat yönü tersi) , yaptığı açının tanjant değerine eşit olur . Eğer alfa açısı dar açı ( 90 dan küçük ) ise eğim pozitif , Eğer alfa açısı geniş ( 90 dan büyük ) ise eğim negatif sayıdır. Eğim = tan a olup, Dik üçgende alfa nın karşısı bölü komşu dik kenar olur. m = 5 / 2 |
|||||||||||||||||
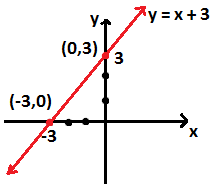
9) y = x + 3 doğrusunun grafiğini çiziniz.
|
Çözüm :
Denklemi verilen doğrunun grafiğini çizmek için , doğrunun geçeceği noktaları belirlemek bulmak gerekir. x e rastgele değerler verip , bu değerleri verilen denklemde x in yerine yazarak , karşılık gelen y değerleri bulunup , Doğrunun dik koordinat düzleminde , geçeceği noktalar tespit edilir. x = 0 için y = 0 + 3 =3 ise Bulunan nokta ( 0 , 3 ) olur. Doğru y eksenini 3 te keser. y = 0 için 0 = x + 3 olup x = -3 olur. İkinci nokta ( - 3 , 0 ) olur ki , bu noktada , doğrunun x eksenini kestiği nokta olur. Noktalar koordinat düzleminde belirlenerek verilen doğrunun denklemi çizilir. |
|||||||||||||||||
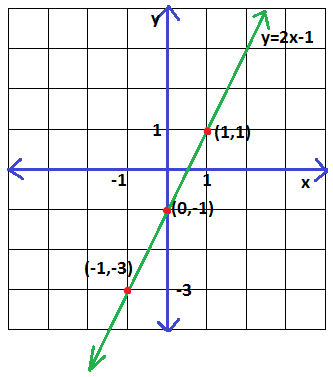
10) y = 2x - 1 doğrusunun grafiğini çiziniz.
|
Çözüm :
x = 0 için y = 2 .0 -1 = -1 olup ( 0 , -1 ) x = 1 için y = 2 . 1 - 1 = 1 ise ( 1 , 1 ) x = -1 için y = 2 .( -1 ) - 1 = -2 - 1 = -3 ise ( -1 , -3 ) noktalar analitik düzlemde birleştirilince, doğrusal denklemin grafiği çizilmiş olur. |
|||||||||||||||||
İki nokta arasındaki uzaklık ile ilgili çözümlü sorular ; Eğimi ve bir noktası bilinen doğrunun denklemini yazma ile ilgili çözümlü sorular .
| Devamı .. | |||
| Analitik Geometri Çözümlü Sorular 1 | Analitik Geometri Çözümlü Sorular 2 | Analitik Geometri Çözümlü Sorular 3 | Analitik Geometri Çözümlü Sorular 4 |