Kümeler
Küme : İyi tanımlanmış nesneler topluluğuna küme denir .
Kümeler A , B , C , ..... gibi büyük harflerle adlandırılır.
c harfi bir A kümesinin elemanı ise c ∈ A ile ifade edilip ,
c elemanıdır A kümesinin diye okunur.
A kümesinin eleman sayısı S(A) şeklinde yazılır .
Örnek :
A = { a , b , c , d , e } , S(A) = 5 elemanlıdır.
Kümelerin Gösterimi :
1 ) Liste Yöntemi :
Kümenin elemanları aralarına virgül konularak küme parantezi içinde yazılır . Bir eleman iki kez yazılmaz.
A = { a , b , c , 1 , 2 , 3 }
B = { a , b , { c , d } , e } kümesi 5 değil 4 elemanlı bir kümedir.
a ∈ B , b ∈ B , { c, d } ∈ B , e ∈ B olur. S (B )= 4
2) Ortak Özellik Yöntemi :
Kümenin elemanları tek tek yazılarak değil de ,
elemanların herkes tarafından aynı anlaşılacak şekilde ifade edilmesi durumudur.
Örnek :
H = { Haftanın Günleri } , kümesi 7 elemanlı bir kümedir .
Örnek :
A = { Alfabe deki sesli harfler } , 8 elemanlı bir kümedir .
Örnek :
A = { x : 3 < x < 10 , x Doğal sayı } , kümesi ,
x öyle ki, 3 küçüktür x küçüktür 10 , ve x doğal sayıdır .. diye okunur .
Bu durumda A kümesinin elemanlarını liste yöntemi ile yazalım ,
A = { 4 , 5 , 6 , 7 , 8 , 9 } olup , S ( A ) = 6 elemanlıdır.
Örnek :
A = { x : 3 ≤ x ≤ 10 , x ∈ N } ise
A kümesi kaç elemanlıdır?
A = { 3,4,5,6,7,8,9,10 } olup S(A) = 8 elemanlıdır.
Örnek :
A = { x : -2 ≤ x < 5 , x ∈ N } ise
A kümesi kaç elemanlıdır?
A kümesinin elemanları -2 ile 5 arasındaki doğal sayılardır . (5 alınmaz.)
A = {0,1,2,3,4} S(A) = 5 olur.
Örnek :
A = { x : -2 ≤ x < 5 , x ∈ Z } ise
A kümesi kaç elemanlıdır?
A kümesinin elemanları -2 ile 5 arasındaki Tam sayılardır . (5 alınmaz.)
A = {-2,-1,0,1,2,3,4} S(A) = 7 olur.
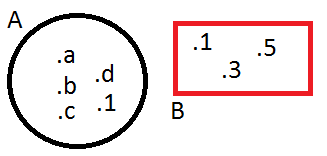
3) Venn Şeması Yöntemi :
Kümenin elemanları kapalı bir şekil içine,
kenarlarına nokta konularak elemanlar yazılır.
Örnek :
Küme Çeşitleri :
1 ) Sonlu Küme , Sonsuz Küme :
Elemanları sayılabilir sayıda olan kümelere sonlu küme denir.
A = { Rakamlar } ise S(A)= 10 eleman vardır.
Elemanları sayılamayan sayıda , sonsuz sayıda olan kümelere sonsuz küme denir.
Örneğin; Doğal sayılar kümesi , Tam sayılar kümesi sonsuz kümelerdir.
N ={0,1,2,3,4,.......}
2 ) Eşit Küme :
Aynı elemanlardan oluşan kümeler eşit kümeler dir.
A = {1,2,3,4} , B = {1,2,3,4} ise A ve B eşit kümelerdir. A = B
S(A) = S(B)=4 , Eleman sayılarıda eşit olur.
3) Denk Kümeler :
Farklı elemanlardan oluşan , ve eleman sayıları aynı ise ,
Denk kümeler denir.
A = {1,2,3} , B = {a,b,c} ise A ≡B , Adenktir B okunur.
4) Boş Küme :
Hiçbir elemanı olmayan kümeye boş küme denir.
{ } yada ∅ sembolü ile gösterilir.
A = ∅ ise S(A) = 0 dır.
Örnek ;
A = { X : -3 < x < 0 , x ∈ N } kümesinin eleman sayısı kaçtır?
A kümesinin elemanlar hem negatif sayılar , hemde doğal sayı olduğu yazıyor.
Doğal sayılar negatif değildir. A = ∅ olup S(A) = 0 dır.
ALT KÜME
Bir kümenin elemanlarından oluşturulan yeni kümelere alt kümeler denir.
B kümesinin elemanlarının hepsi A kümesinin de elemanı ise,
B kümesi A kümesinin alt kümesidir denir ve
B ⊂ A şeklide gösterilir.
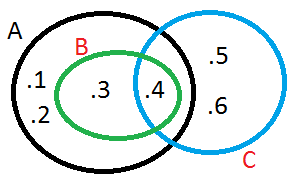
Şekilde B ⊂ A dir. C ⊄ A ( B alt kümesidir A , Fakat C alt kümesi değildir A)
Örnek :
A = { a,b,c,d } kümesinin alt kümelerini yazalım.
|
0 Elemanlı Alt Kümeler |
1 Elemanlı Alt Kümeler |
2 Elemanlı Alt Kümeler |
3 Elemanlı Alt Kümeler |
4 Elemanlı Alt Kümeler |
| { } |
{a} {b} {c} {d} |
{a,b} {a,c} {a,d} {b,c} {b,d} {c,d} |
{a,b,c} {a,b,d} {a,c,d} {b,c,d} |
{a,b,c,d} |
| C(4,0)=1 tane |
C(4,1)=4 tane |
C(4,2)=6 tane |
C(4,3)=4 tane |
C(4,4)=1 tane |
A kümesinin Toplam 1+4+6+4+1 =16 tane alt kümesi vardır.
Alt küme sayısı 24 = 2.2.2.2 = 16 tane olur.
ALT KÜME SAYISI HESAPLAMA
n elemanlı bir kümenin alt küme sayısı 2n formülü ile bulunur.
Öz alt küme:
Bir kümenin kendisi dışındaki diğer alt kümeleri öz alt kümelerdir.
Öz alt küme sayısı 2n - 1 formülü ile bulunur. (Kendisini saymıyoruz.)
Örnek :
3 elemanlı bir kümenin alt küme sayısı ve özalt küme sayısı kaçtır?
Çözüm :
23 = 2.2.2= 8 alt kümesi ve 8 -1 = 7 tane de özalt kümesi vardır.
Örnek :
128 tane alt kümesi olan bir küme kaç elemanlıdır?
Çözüm :
128 :2 = 64 , 64 :2 =32 , 32:2 = 16 , 16 : 2=8 , 8:2 =4 , 4:2 =2 , 2:2=1 ise,
128 sayısı 7 kez 2 ye bölündü.
2n = 128 ise 2n = 27 ise n=7 elemanlıdır.
Örnek :
Alt küme ve öz alt küme sayısı toplamı 63 olan küme kaç elemanlıdır?
Çözüm :
2n + 2n - 1 = 63 ise
2. 2n - 1 =63
2. 2n=63+1 ise 2. 2n =64 ise 2n =32 olup n=5 elemanlı olur.
Örnek :
A = { a,b,c,d } kümesinin alt kümelerini yazalım.
|
0 Elemanlı Alt Kümeler |
1 Elemanlı Alt Kümeler |
2 Elemanlı Alt Kümeler |
3 Elemanlı Alt Kümeler |
4 Elemanlı Alt Kümeler |
| { } |
{a} {b} {c} {d} |
{a,b} {a,c} {a,d} {b,c} {b,d} {c,d} |
{a,b,c} {a,b,d} {a,c,d} {b,c,d} |
{a,b,c,d} |
Sorular:
Yukarıda verilen A = { a,b,c,d } kümesinin;
a) Kaç tane alt kümesi vardır?
24 =16
b) 2 elemanlı kaç tane alt kümesi vardır?
C(4,2)= 6 tane.
c) En çok 2 elemanlı alt küme sayısı kaçtır?
0 elemanlılar+ 1 elemanlılar + 2 elemanlı alt kümeler (Kombinasyon ile hesaplanır.)
C(4,0)+C(4,1)+C(4,2)=1+4+6=11 tane
