Kümeler 9. sınııf test çözümleri , kümelerde kesişim birleşim fark işlemleri anlatılmaktadır.
Kumeler 2
Soru 1
A = { 1 , 2 } ve B = { 1 , 2 , 4 , 5 }
olduğuna göre A ∪ B birleşim kümesi hangisidir?
| A) { 1 , 2 } |
| B) { 1 , 2 , 4 , 5 } |
| C) { 4 , 5 } |
| D) { 1 , 2 , 3 , 4 , 5 } |
| E) { 1 , 1 , 2 , 2 , 4 , 5 } |
Çözüm:
İki kümenin birleşim kümesi her iki kümenin
elemanlarının birleştirilmesiyle oluşur.
Her iki kümede de var olan ortak elemanlar
birleşim kümesine bir kez yazılır. Buna göre;
A U B = { 1, 2 , 4 , 5 } olur.
Cevap : B
Soru 2
A = { 3 , 4 , 5 } , B = { 1 , 2 , 3 , 5 }
kümeleri için A ∩B kesişim kümesi hangisidir?
| A) { 3 } |
| B) { 1 , 2 , 3 , 4 , 5 } |
| C) { 3 , 5 } |
| D) { 4 , 5 } |
| E) { 2, 3 , 5 } |
Çözüm:
Kesişim kümesi her iki kümede de olan
ortak elemanlardan oluşan kümedir.
A ∩ B = { 3 , 5 }
Cevap : C
Soru 3
A = { a , b , c , d } ve B = {b , c , e}
olduğuna göre A \ B fark kümesi hangisidir?
| A) { a , b , c , d} |
| B) { b , c , e } |
| C) { a , c , d } |
| D) { e } |
| E) { a , d } |
Çözüm:
A \ B yada A - B , yani A fark B kümesi demek ,
A kümesinden ortak elemanları çıkarınca geriye kalan
elemanlar A fark B kümesinin elemanları olur.
A \ B = A - B = { a , b , c , d } - { b , c }
A \ B = { a , d } olur.
Cevap : E
Soru 4
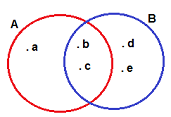
Şekilde verilen A ve B kümeleri için
aşağıdakilerden hangisi yanlıştır?
| A) A = { a } |
| B) B = { b , c , d , e } |
| C) A ∪ B = { a , b , c , d , e} |
| D) A ∩ B = { b , c } |
| E) S ( AUB ) = 5 |
Çözüm:
Cevap : A
Soru 5
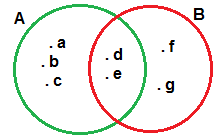
Şekilde verilen A ve B kümeleri için
I. A ∩ B = { d , e }
II . A \ B = { f , g }
III . B \ A = { d , e , f , g }
IV . ( A ∩ B ) \ B = ∅
ifadelerinden hangileri doğrudur?
| A) I ve IV | B) I,II , III | C) II ve IV |
| D) Yalnız I | E) Yalnız II |
Çözüm:
Cevap : A
| Devamı .. | ||
| Kümeler Çözümlü Sorular 1 | Kümeler Çözümlü Sorular 2 | Kümeler Çözümlü Sorular 3 |
| Kümeler Çözümlü Sorular 4 | ||
KÜMELERDE İŞLEMLER
1. Kümelerde Birleşim işlemi:
İki yada daha fazla kümenin elemanlarının birleşmesiyle oluşan yeni kümeye birleşim kümesi denir.
Birleşim işlemi U sembolü ile gösterilir.
A ile B kümelerinin birleşimi A U B ile gösterilir ve A birleşim B diye okunur.
A U B ={ x | x ∈ A veya x ∈ B } dir.
2. Kümelerde Kesişim işlemi:
İki yada daha fazla kümenin ortak elemanlarından oluşan yeni kümeye kesişim kümesi denir .
Kesişme işlemi ∩ sembolü ile gösterilir.
A ile B kümelerinin kesişimi A ∩ B ile gösterilir ve A kesişim B diye okunur.
A ∩ B ={ x | x ∈ A ve x ∈ B } dir.
Birleşim ve Kesişim işleminin özellikleri:
1) A U A = A ( Bir kümenin kendisi ile birleşimi yine kendisine eşittir.)
A ∩ A = A ( Bir kümenin kendisi ile kesişimi yine kendisine eşittir.)
2) A U ∅ = A ( Bir kümenin boş küme ile birleşimi kendisine eşittir.)
A ∩ ∅ = ∅ ( Bir kümenin boş küme ile kesişimi boş kümeye eşittir.)
3) A U (BUC)= ( AUB ) U C (Birleşme özelliği vardır.)
A ∩ (B ∩ C)= ( A ∩ B ) ∩ C
4) A U B = B U A ( Değişme özelliği, yer değiştirme vardır.)
A ∩ B = B ∩ A
5) A U E = E ( Bir kümenin evrensel küme ile birleşimi evrensel kümedir.)
A ∩ E = A ( Bir kümenin evrensel küme ile kesişimi kendisine eşittir.)
6) B ⊂ A ise A U B = A ve A ∩ B = A
7) Dağılma özelliği:
A U ( B ∩ C ) = (A U B) ∩ ( AU C ) ( Birleşimin kesişim üzerine dağılması )
A ∩ ( B U C ) = ( A ∩ B ) U ( A ∩ C ) ( Kesişimin birleşim üzerine dağılması)
8) De Morgan Kuralları :
( AUB )’ = A’ ∩ B’ ve ( A ∩ B )’ = A ‘ U B’
9) Birleşim kümesinin eleman sayısı formülü:
S ( AUB ) = S(A) + S (B) - S ( A ∩ B )
Üç kümenin birleşimi:
S(AU B U C) = S(A) + S (B) +S (C) - S( A ∩ B) -S ( A ∩ B) - S ( B ∩ C )+ S( A ∩ B ∩ C)
Devamı..
KONU
KÜMELER
TEST
Alt küme soruları
KÜMELER ÇÖZÜMLÜ SORULAR1
TEST1
Kümelerde işlemler soruları
KÜMELER ÇÖZÜMLÜ SORULAR 2
TEST2
Küme problemleri soruları
KÜMELER ÇÖZÜMLÜ SORULAR 3
Küme problemleri soruları
ÇÖZÜMLÜ SORULAR 4
Küme problemi çözümü şekilli
ÇÖZÜMLÜ SORULAR 5
Küme Problemleri Soruları Şekilli Çözümler.
ÇÖZÜMLÜ SORULAR 6
