8. sınıfta da permütasyon konusu işlenmektedir.
1) P( 5 , 2 ) = ? |
Çözüm :
|
||||||||||||||||
2) P( n , 2 ) = 42 olduğuna göre n kaçtır?
|
Çözüm :
n . (n-1) = 42 ise kendisi ile 1 eksiğinin çarpımı 42 olan sayı 7 olur. 7 . ( 7 - 1 )=42 n = 7 bulunur. |
||||||||||||||||
3) P( n-3 , 1 ) = 10 olduğuna göre n kaçtır?
|
Çözüm :
(n-4) ler sadeleşir. n - 3 = 10 ise n = 10 + 3 n = 13 bulunur. |
||||||||||||||||
4) P( n+1 , n-4 ) = 6 olduğuna göre n kaçtır?
|
Çözüm :
içler dışlar çarpımından (n+1)! = 6 . 5 ! (n+1)! = 6 ! n + 1 = 6 n = 6 -1 n= 5 olur. |
||||||||||||||||
5 ) 5 kişilik bir aile yan yana fotoğraf çekilecektir .Kaç farklı şekilde çekilebilir?
|
Çözüm : 5 kişinin yan yana 5 li sıralanışları yani, 5 kişinin 5 li permütasyonları söz konusudur.
P ( 5 , 5 ) = 5 ! = 5.4.3.2.1 = 120 farklı şekilde çekim yapılır. Sonuç : 5 kişi yan yana 5 ! şekilde sıralanır. 7 kişi olsaydı yan yana 7 ! şekilde sıralanabilir. |
||||||||||||||||
6 ) 5 kişilik bir aile yan yana 3 kişilik olarak fotoğraf çekilecektir . Kaç farklı şekilde çekilebilir?
|
Çözüm : 5 kişinin yan yana 3 lü sıralanışları yani, 5 kişinin 3 lü permütasyonları söz konusudur.
P ( 5 , 3 ) = 5 .4.3.2.1 / 2 .1 = 5.4.3 = 60 farklı şekilde çekim yapılır. |
||||||||||||||||
7 ) 7 kişilik bir aile yan yana 4 koltuğa oturup fotoğraf çekilecektir . Kaç farklı şekilde çekilebilir?
|
Çözüm : Yukardaki soruya çok benzer. 7 kişinin yan yana 4 lü sıralanışları yani, 7 kişinin 4 lü permütasyonları söz konusudur.
P ( 7 , 4 ) = 7. 6. 5 .4.3.2.1 / 3 . 2 .1 = 7 . 6 . 5 . 4 = 840 farklı şekilde çekim yapılır. 2 yol pratik olarak , kutu metodu ile , 1.koltuğa 7 seçenek var , 2 . koltuğa 6 seçenek , 3. koltuğa 5 yol kalır , 4 . koltuğa 4 kişi kalırsa, cevap : 7.6.5.4 = 840 farklı diziliş olur. |
||||||||||||||||
8) 8 kişinin katıldığı bir koşu yarışında , birinci, ikinci, üçüncü kaç değişik şekilde oluşabilir?
|
Çözüm : birincilik için 8 alternatif kişi, ikincilik için 7 kişi kalır , üçüncülük için ise 6 farklı seçenek vardır. cevap : 8 .7 . 6 = 336 farklı şekilde oluşabilir. |
||||||||||||||||
9 ) 30 kişilik bir sınıfta bir başkan birde yardımcı kaç farklı şekilde seçilebilir? |
Çözüm : 30 . 29 = 870 farklı şekilde. |
||||||||||||||||
10) 3 mektup 4 posta kutusuna atılıyor . a) Kaç farklı şekilde atılabilir? b) Her kutuda en çok bir mektup olması koşulu ile kaç farklı şekilde atılır?
|
Çözüm : a ) 4 kutu var ise , her bir mektup için 4 farklı yol vardır. Buna göre , 1. mektup için 4 yol , 2 . mektup için 4 yol , Üçüncü mektup için de 4 yol var ise. 4 . 4 . 4 = 4 3 = 64 b ) Her kutuda en çok 1 mektup olur, yada 0 mektup olur. Bir mektup atılınca, diğer kutulara atılamayacağından mektup sayısı azalacaktır. Buna göre cevap ; Birinci mektup için 4 yol , ikinci mektup için 3 yol , üçüncü mektup için 2 yol kalır . 4 . 3 . 2 = 24 farklı şekilde atılır. |
||||||||||||||||
11) 4 Kız , 3 Erkek bir sırada yanyana ; a) Kaç farklı şekilde sıralanır ? b ) Kızlar bir arada olmak şartıyla kaç farklı şekilde sıralanırlar? c ) Kızlar bir arada ve Erkekler bir arada olmak koşulu ile kaç türlü sıralanırlar?
|
Çözüm : a ) 4 + 3 = 7 kişi yanyana 7 ! şekilde sıralanır. b ) 4 Kız bir kişi sayılır . 1 + 3 E = 4 kişi yan yana 4 ! = 24 şekilde. c ) 4 kız 1 kişi , 3 erkek 1 kişi sayılıp , 2 kişi 2! olur . Ancak kızlar kendi arasında 4! yer değiştirir. erkeklerde 3! O halde cevap 2 ! . 4 ! . 3 ! |
||||||||||||||||
|
12) 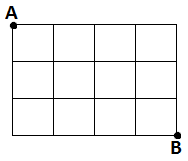
Şekilde A noktasından B noktasına en kısa yoldan kaç farklı şekilde gidilir?
|
Çözüm : 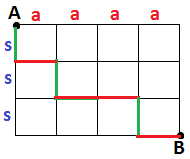
Tekrarlı permütasyon sorusu oluyor. A dan B ye yatay olarak 4 çizgi , düşey olarak ta 3 çizgi vardır. En kısa yoldan gitmek için 4 tane yatay 3 tane de düşey çizgi kullanılacaktır. 4+3 = 7 olur. aaaasss , aassaas , ... gibi gidilecek. Tekrarlı permütasyon kuralına göre 7 ! / 4 ! . 3! = 7.6.5/3.2.1 = 35 35 farklı yoldan gidilir. Cevap : 35 |
||||||||||||||||
