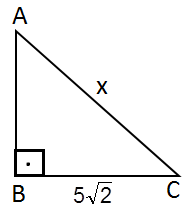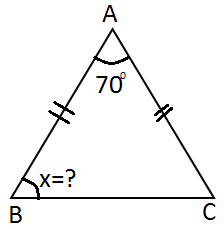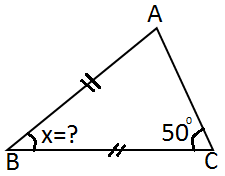Özel üçgenler çözümlü sorular , 30-60-90 üçgeni , 45-45-90 üçgeni , ygs lys kpss soru çözümü hazırlık.
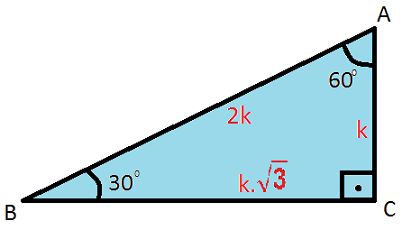
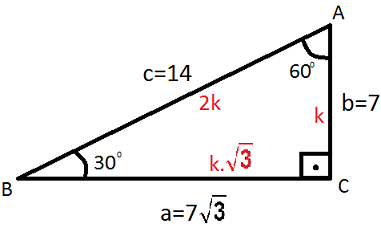
30-60-90 üçgeni kenar uzunlukları bulma. |
|||||
|
--30 derecenin karşısındaki kenarın uzunluğu hipotenüs uzunluğunun yarısına eşit olur. ---60 derecenin karşısındaki kenarın uzunluğu ise hipotenüsün yarısı alınıp birde kök 3 ile çarpılarak bulunur. |
Örnek:
|
||||
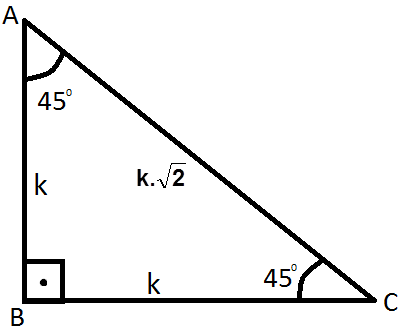
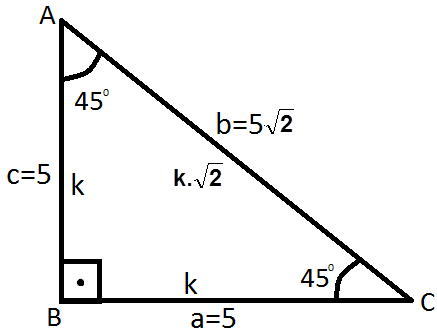
45-45-90 üçgeni ( ikizkenar dik üçgen ): |
|||||
|
-- İkizkenar dik üçgende hipotenüs uzunluğu , 45 derecenin karşısındaki kenar uzunluğunun kök 2 ile çarpımına eşit olur. |
Örnek:
|
||||
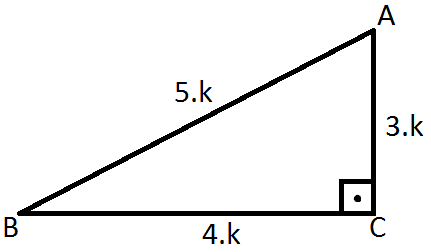
Özel dik üçgenler 3-4-5 üçgeni : |
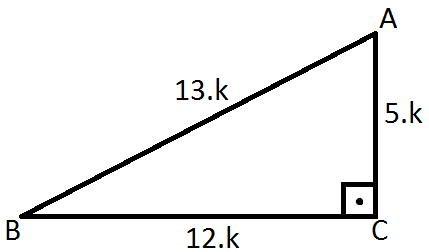
Özel dik üçgenler 5-12-13 üçgeni : |
||||
|
|
Aynı şekilde kenar uzunlukları 5 in 12 nin ve 13 ün katı olan üçgenler de özel dik üçgenlerdir, Ayrıca kenar uzunlukları 8-15-17 ve katları olan üçgenlerde pisagor bağıntısına göre, özel dik üçgen olmaktadır.
|
||||
1) Şekildeki ikizkenar dik üçgende verilenlere göre |AC|=x uzunluğu kaçtır?
|
Çözüm: İkiz kenar dik üçgen 45-45-90 üçgeni olup dik kenar uzunlukları eşittir. 90 nın karşısı 45 in karşısının kök 2 katı dır.
x = 5 . 2 x = 10 olur. |
|
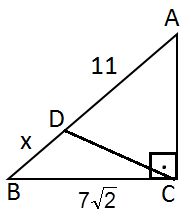
2) Şekildeki ikizkenar dik üçgende verilenlere göre |BD|= x kaçtır?
|
Çözüm: 45-45- 90 üçgeninde 90 derecenin karşısı dik kenarın √2 ile çarpımına eşittir. |AB| = 7 √2 . √2 |AB| = 7 . 2 |AB| = 14 |BD| = 14 - 11 |BD| = 3 |
|
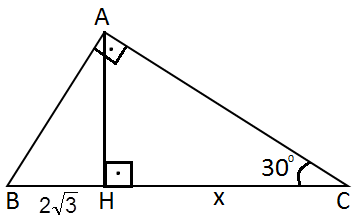
3) Şekilde verilenlere göre |HC|= x nedir?
|
Çözüm : m(B)= 60 olur. m(BAH)=30 olur. |AB| = 2 . 2 √3 |AB| = 4 √3 |BC| = 2 . 4 √3 |BC| = 8 √3 x = 8 √3 - 2 √3 x = 6 √3
|
|
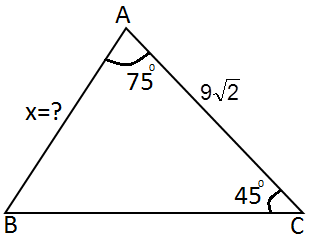
4) Şekilde verilenlere göre |AB|= x nedir?
|
Çözüm : A noktasından dikme indirilir. İkizkenar dik üçgende |AH|= 9 olur. 30 - 60 - 90 üçgeninde , |BH|= 9/ √3 |AB |= 2 . 9/ √3 = 18 / √3 = 18 . √3 / 3 |AB |= 6 √3
|
|
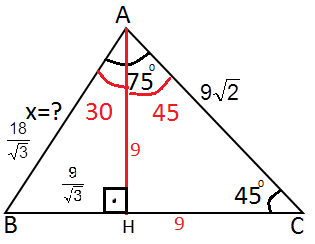
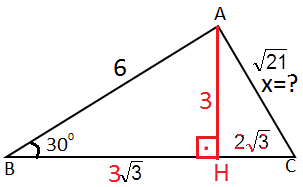
5) Şekilde verilenlere göre |AC|= x nedir?
|
Çözüm : A noktasından dikme indirilir. 30-60 -90 üçgeninde |AH|= 3 olur. |BH|= 3 √3 olur. |HC |= 5 √3 - 3 √3 = 2 √3 AHC üçgeninde , x 2 = 3 2 + ( 2 √3 ) 2 x 2 = 9 + 12 x 2 = 21 x = √21 |
|
6) Şekildeki ikizkenar üçgende verilenlere göre m(ABC)= x açısı kaç derecedir?
|
Çözüm: İkizkenar üçgende taban açıları m ( B ) = m ( C ) eşit olur. Buna göre m(B)= (180 - 70 )/ 2 m(B) = 110 / 2 m(B) = 55 |
|
7) Şekildeki ikizkenar üçgende verilenlere göre m(ABC)= x açısı kaç derecedir?
|
Çözüm: İkizkenar üçgende taban açıları m ( A ) = m ( C ) = 50 eşit olur. Buna göre m(B) + 50 + 50 = 180 x + 100 = 180 x= 180 - 100 x= 80
|
|
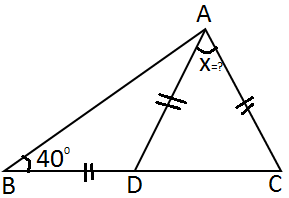
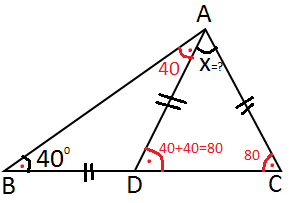
8) Şekilde verilenlere göre m(CAD)= x açısı kaç derecedir?
|
Çözüm : İkizkenar üçgende taban açıları eşittir. m (ABD) = m (DAB) = 40 olur. İki iç açının toplamı üçüncü köşedeki dış açıyı verir. m (ADC) = 40+40 = 80 olur. x = 180 - ( 80 + 80 ) x= 180 - 160 = 20 derece. |
|
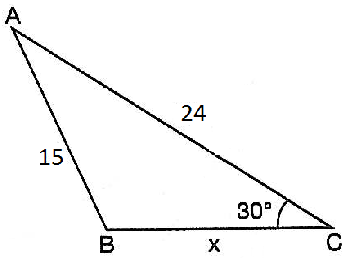
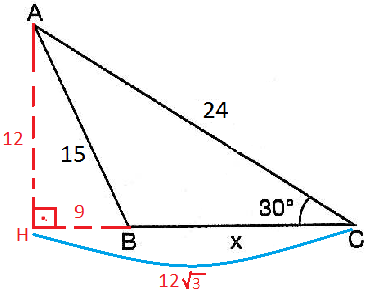
9) Şekilde |BC| = 24 ise verilenlere göre |AC|= ? nedir?
|
Çözüm : A noktasından dikme indirilir. ABD ikizkenar üçgende taban açılar eşit x dersek, D açısı 2x ve C açısıda x olur . AHC üçgeni 30 - 60 - 90 üçgeni olur . ( 2x+x=90 ) AH = 12 / √3 |AC|= 2 . 12 / √3 = 24 / √3 = (24 . √3) / 3 |AC|= 8 √3 |
|
10) Şekilde verilenlere göre |BC|=x nedir?
|
Çözüm : A noktasından dikme indirilir. AHC üçgeni 30 - 60 - 90 üçgeni olur . |AH|= 24 / 2 =12 olur. AHB üçgeni 3-4-5 in 3 katı 9-12-15 olur. x = 12√3 - 9 olur. |
|